算法题（四）

本文最后更新于：2022年5月31日 下午

概览：LeetCode刷题。

1
2
3
4
<details>
    <summary>折叠/查看代码</summary>
    
</details>

剑指 数组中只出现1次的数 | 祖龙面试

折叠/查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//题目：一个数组中，许多数字出现两次，只有一个数字出现1次
//思路：异或算法，相异为1，相同为0
//那么重复的元素和自已相异或就会抵消

int main() {

    vector<int> nums = { 1,2,3,1,2,3,4,5,6,7,7,6,5 };

    int result = nums[0];
    int len = nums.size();
    for (int i = 1; i < len; i++) {
        result = result ^ nums[i];
    }

    cout << result << endl;//4
    return 0;
}

23 合并K个升序链表

2021/04/16

给你一个链表数组，每个链表都已经按升序排列。

请你将所有链表合并到一个升序链表中，返回合并后的链表。

示例 1：

输入：lists = [[1,4,5],[1,3,4],[2,6]]
输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下：
[
1->4->5,
1->3->4,
2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6
示例 2：

输入：lists = []
输出：[]
示例 3：

输入：lists = [[]]
输出：[]

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/merge-k-sorted-lists
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

  • 思路1：采用两两归并的思想，逐步归并到一起。
  • 思路2：获取链表的全部元素，排序成数组，然后构建链表
    • 空间占用优点过多。
  • 思路3：优先级队列，每次选择所有链表中元素最小的那个，直到合并完毕！

可以采用优先级队列，都暂时存放一系列链表中的第一个数，排序出其中最小的那个元素.

当将那个元素加入链表后，就将原来元素的下一个链表插入到队列中.

折叠/查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class Solution {
public:
    struct Status{
        int val;
        ListNode* ptr;
        Status(int vval,ListNode* vptr){
            val = vval;
            ptr = vptr;
        }
        bool operator<(const Status &other) const{//记得重载运算符
            return val>other.val;
        }
    };

    priority_queue<Status> que;

    ListNode* mergeKLists(vector<ListNode*>& lists) {
        //若链表数量为1，直接返回
        int len = lists.size();
        if(len == 0) return nullptr;
        else if(len == 1) return lists[0];

        //若有多个链表
        //初始化一个链表，然后逐个访问每个链表的节点，
        for(auto i : lists){
            if(i != nullptr){
                que.push({i->val,i});
            }
        }
        ListNode * head = new ListNode();//当作头节点

        ListNode* nodes = head;

        while(!que.empty()){
            Status i = que.top();
            que.pop();
            head->next = i.ptr;
            head = head->next;

            if(i.ptr->next != nullptr) que.push({i.ptr->next->val,i.ptr->next});
        }

        return nodes->next;
    }
};

53 最大子序和 | 祖龙面试

2021/04/18

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例 1：

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。
示例 2：

输入：nums = [1]
输出：1
示例 3：

输入：nums = [0]
输出：0
示例 4：

输入：nums = [-1]
输出：-1
示例 5：

输入：nums = [-100000]
输出：-100000

提示：

1 <= nums.length <= 3 * 104
-105 <= nums[i] <= 105

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/maximum-subarray
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

面试时的写法

面试时想到了动态规划，然后使用了二维的动态规划数组。最后勉强做出来了，但是面试官很不满意。

  • 在力扣实测会超时。尴尬
折叠/查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/*
    思路：二维的动态规划
    dp[i][j]存储i-1这个元素到j-1这个元素的最大和
    dp[i][i]是对角线元素，优先初始化
*/
int maxSubArray(vector<int>& nums) {
    int len = nums.size();
    if(len == 1)
        return nums[0];

    vector<vector<int>> dp(len,vector<int>(len));

    int maxsum = -100001;
    for(int i=0;i<len;i++){
        dp[i][i] = nums[i];
        maxsum = max(maxsum,dp[i][i]);
        for(int j = i+1;j<len;j++){
            dp[i][j] = max(dp[i][j-1]+nums[j],nums[j]);
            maxsum = max(maxsum,dp[i][j]);
        }
    }

    return maxsum;
}

动态规划优化

只需要找到最大值，使用一位的dp数组，就可以解决这个问题，dp[i]存储的是0-i上的最大子序列的和。

折叠/查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int maxSubArray(vector<int>& nums) {
    int len = nums.size();
    if(len == 1)
        return nums[0];
    vector<int> dp(len);

    int maxsum = nums[0];
    dp[0] = nums[0];
    for(int i=1;i<len;i++){
        dp[i] = max(nums[i],dp[i-1]+nums[i]);
        maxsum = max(maxsum,dp[i]);
    }

    return maxsum;
}

动态规划再优化

将上述dp[i]的思想再进行优化，使用O(1)的空间，使用一个变量去保存之前的最大值即可。

折叠/查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
int maxSubArray(vector<int>& nums) {
    int len = nums.size();

    int sum = nums[0];
    int maxsum = nums[0];
    for(int i=1;i<len;i++){
        sum = max(nums[i],sum+nums[i]);
        maxsum = max(maxsum,sum);
    }

    return maxsum;
}

剑指 旋转数组的最小数字

2021/04/18

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。输入一个递增排序的数组的一个旋转，输出旋转数组的最小元素。例如，数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一个旋转，该数组的最小值为1。

示例 1：

输入：[3,4,5,1,2]
输出：1
示例 2：

输入：[2,2,2,0,1]
输出：0

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/xuan-zhuan-shu-zu-de-zui-xiao-shu-zi-lcof
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路1：直接遍历

找寻非单调递减序列发生变化的地方，那就是最小值！时间 O(n).

折叠/查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
int minArray1(vector<int>& numbers) {
    int ans = numbers[0];

    int len = numbers.size();

    for(int i=0;i<len;i++){
        if(ans <= numbers[i])
            continue;
        else
            return numbers[i];
    }
    return ans;
}

思路2：二分查找

若中间的元素，小于最后一个元素，按照题意，可知这后半段是完全递增的，所以最小值在前半段。

若中间元素，大于最后一个元素，则最小值就在后半段。

若中间元素等于最后一个元素：

  • 22222
  • 22202
  • 20222
  • 02222

对于这些情况，可以更改right的指针来缩减范围，即right指针所指位置，肯定不会是最小元素（元素完全相同不考虑）。

不能更改left，left可能会指向最小值！

时间：O(log n)

折叠/查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int minArray(vector<int>& numbers) {
    int len = numbers.size();
    int left = 0;
    int right = len-1;
    while(left < right){
        int mid = left + (right-left)/2;
        if(numbers[mid] > numbers[right])
            left = mid+1;
        else if(numbers[mid] < numbers[right])
            right = mid;
        else
            right--;
    }
    return numbers[left];
}

剑指 二叉搜索树转双向链表 | 好未来二面

2021/04/18

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点，只能调整树中节点指针的指向。

为了让您更好地理解问题，以下面的二叉搜索树为例：

我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表，第一个节点的前驱是最后一个节点，最后一个节点的后继是第一个节点。

下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。

特别地，我们希望可以就地完成转换操作。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/er-cha-sou-suo-shu-yu-shuang-xiang-lian-biao-lcof
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路：二叉搜索树，中序遍历是一个递增序列。可通过中序遍历过程中，修改前面节点的指针指向。

当然对头尾两个节点的指针要额外处理，达到双向循环链表的效果。

折叠/查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
/*
树中左指针指向前驱，右指针指向后继
*/
class Solution {
public:
    Node* treeToDoublyList(Node* root) {
        if (root == NULL) return NULL;//若没有节点，直接返回！
        //尝试使用中序遍历
        stack<Node *> st;
        Node * tmp = root;
        Node * pre = NULL;
        Node * head;
        Node * tail;
        while (tmp != NULL || !st.empty()) {
            if (tmp != NULL) {
                st.push(tmp);
                tmp = tmp->left;
            }
            else {
                tmp = st.top();
                st.pop();

                if (pre == NULL) {//当为NULL时，说明还没有被初始化，初始化pre和head节点
                    pre = tmp;
                    head = pre;
                }
                else {			//维护双向链表
                    pre->right = tmp;
                    tmp->left = pre;
                    pre = pre->right;
                }
                tail = tmp;//记录尾节点，当当前节点的右为空时，且栈为空时，就会结束

                tmp = tmp->right;
            }
        }

        //需要将头节点和末尾节点相互进行指向!
        tail->right = head;
        head->left = tail;

        return head;
    }
};

131 分割回文串

2021/04/18

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是 回文串 。返回 s 所有可能的分割方案。

回文串 是正着读和反着读都一样的字符串。

示例 1：

输入：s = “aab”
输出：[[“a”,”a”,”b”],[“aa”,”b”]]
示例 2：

输入：s = “a”
输出：[[“a”]]

提示：

1 <= s.length <= 16
s 仅由小写英文字母组成

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/palindrome-partitioning
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

回溯算法

视频讲解：https://www.bilibili.com/video/BV1c54y1e7k6

折叠/查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution {
public:
    vector<vector<string>> result;
    vector<string> path;

    bool isParl(string & s){
        int len = s.size();
        if(len <= 1) return true;

        int i = 0;
        int j = len-1;

        while(i <= j){
            if(s[i] == s[j]){
                i++;
                j--;
            }else return false;
        }
        return true;
    }

    void trackback(string &s, int start){
        //结束条件
        if(start >= s.size()){
            result.push_back(path);
            return;
        }
        //横向遍历
        for(int i = start;i<s.size();i++){
            //分割字符串，查看其是否是回文串
            string tmp = s.substr(start,i-start+1);
            if(isParl(tmp)){
                path.push_back(tmp);
                trackback(s,i+1);
                path.pop_back();
            }else{
                continue;
            }
        }
    }

    vector<vector<string>> partition(string s) {
        result.clear();
        path.clear();
        trackback(s,0);
        return result;
    }
};

剑指 数据流中的中位数

2021/04/19

如何得到一个数据流中的中位数？如果从数据流中读出奇数个数值，那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值，那么中位数就是所有数值排序之后中间两个数的平均值。

例如，

[2,3,4] 的中位数是 3

[2,3] 的中位数是 (2 + 3) / 2 = 2.5

设计一个支持以下两种操作的数据结构：

void addNum(int num) - 从数据流中添加一个整数到数据结构中。
double findMedian() - 返回目前所有元素的中位数。
示例 1：

输入：
[“MedianFinder”,”addNum”,”addNum”,”findMedian”,”addNum”,”findMedian”]
[[],[1],[2],[],[3],[]]
输出：[null,null,null,1.50000,null,2.00000]
示例 2：

输入：
[“MedianFinder”,”addNum”,”findMedian”,”addNum”,”findMedian”]
[[],[2],[],[3],[]]
输出：[null,null,2.00000,null,2.50000]

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/shu-ju-liu-zhong-de-zhong-wei-shu-lcof
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路1：排序，然后找到中位数，但是对于这种数据流不断增加的数组来说，每次都需要重新排序，每次O(nlog n).

思路2：使用堆排序，构建两个数量几乎相同的堆，一个小顶堆一个大顶堆，小顶堆的全部元素都大于等于大顶堆的堆顶元素。这样数据的中位数都在两个堆顶之间产生。而每次调整堆的时间复杂度是O(logn)，每次至多调整两个堆，这样的时间复杂度仍然小于排序的。

折叠/查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
class MedianFinder {
public:
    /** initialize your data structure here. */

    vector<int> min;
    vector<int> max;

    MedianFinder() {
        min.clear();
        max.clear();
    }

    void addNum(int data) {
        if (min.size() > max.size()) {
            //插入到大根堆

            //同时还要保证 该元素要有序
            if (data > min[0]) {
                //若大于等于小根堆的最小元素，则小根堆元素先弹出
                pop_heap(min.begin(), min.end(), greater<int>());
                int tmp = min.back();
                min.pop_back();

                //将元素插入小根堆
                min.push_back(data);
                push_heap(min.begin(), min.end(), greater<int>());
                data = tmp;
            }

            max.push_back(data);
            push_heap(max.begin(), max.end(),less<int>());
        }
        else {
            //此时 要么元素数量相同，都为0，或者都为一定数目
            if (min.size() == 0) {
                min.push_back(data);
                push_heap(min.begin(), min.end(), greater<int>());
            }

            else {
                    //先插入大根堆
                    max.push_back(data);
                    push_heap(max.begin(), max.end(), less<int>());

                    //先将大根堆元素插入小根堆
                    pop_heap(max.begin(), max.end(), less<int>());
                    int tmp = max.back();
                    max.pop_back();

                    min.push_back(tmp);
                    push_heap(min.begin(), min.end(), greater<int>());

                }
            }
        }

    double findMedian() {
        if (((min.size() + max.size()) & 1) == 1) {
            return min[0];
        }
        else {
            return (min[0] + max[0]) / 2.0;
        }
    }
};

206 翻转链表

2021/04/21

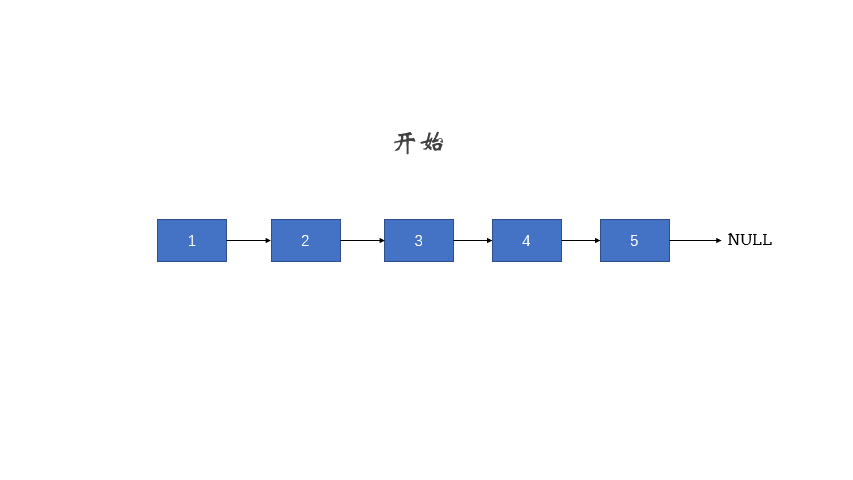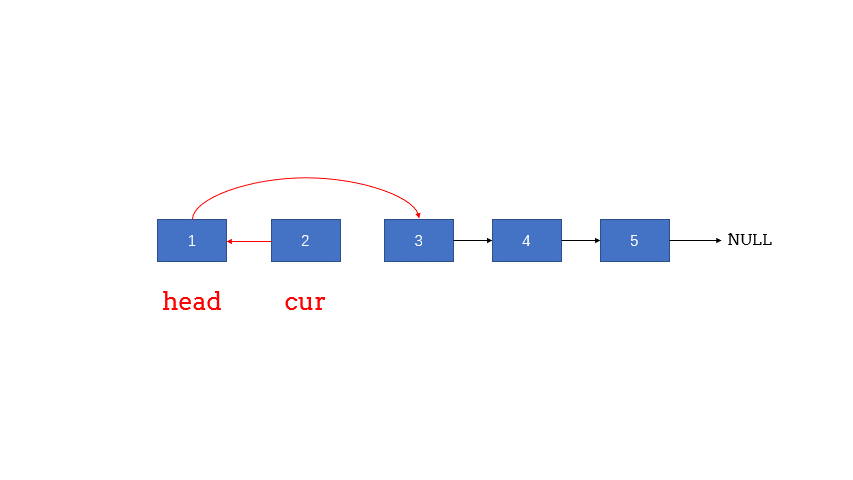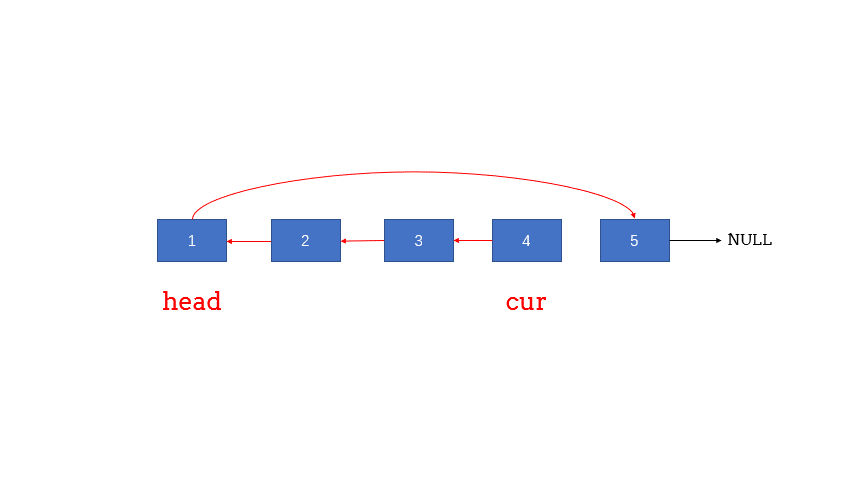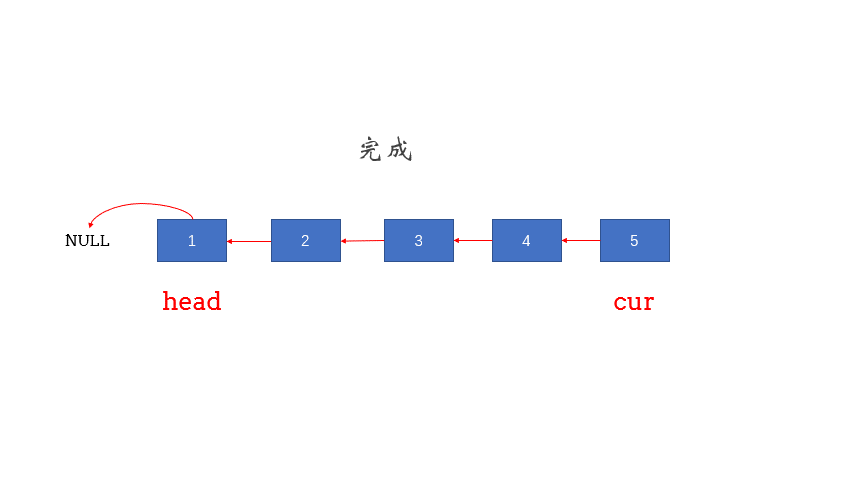
反转一个单链表。

示例:

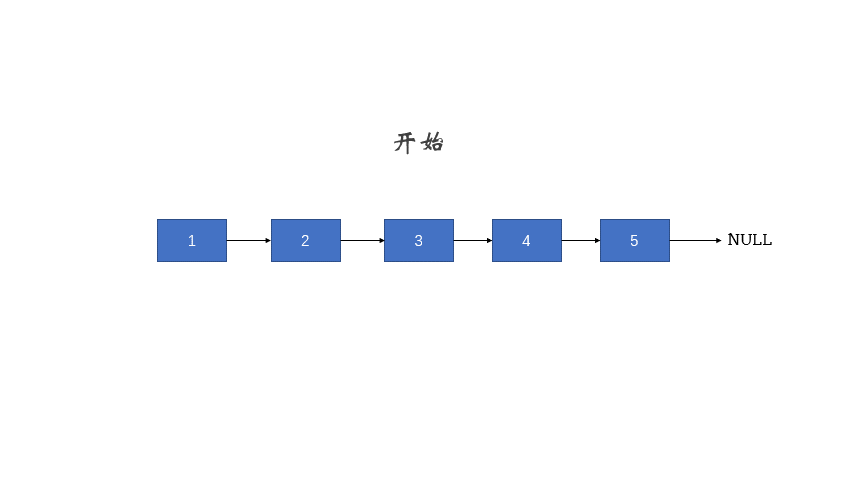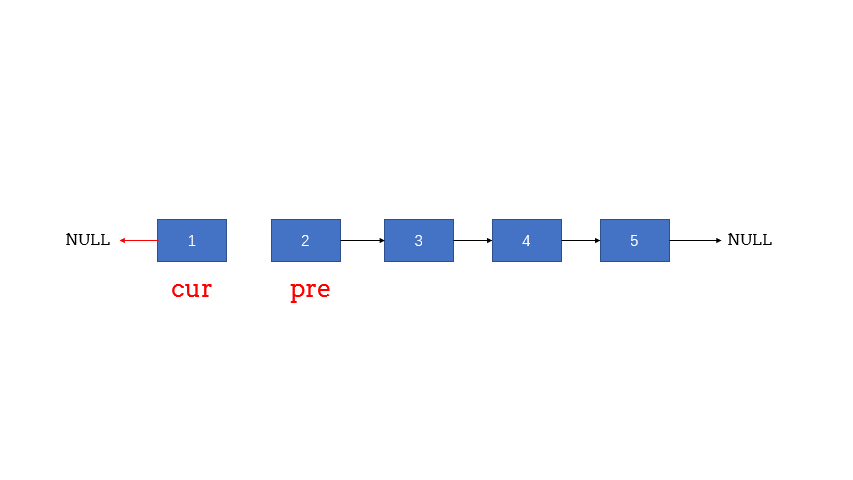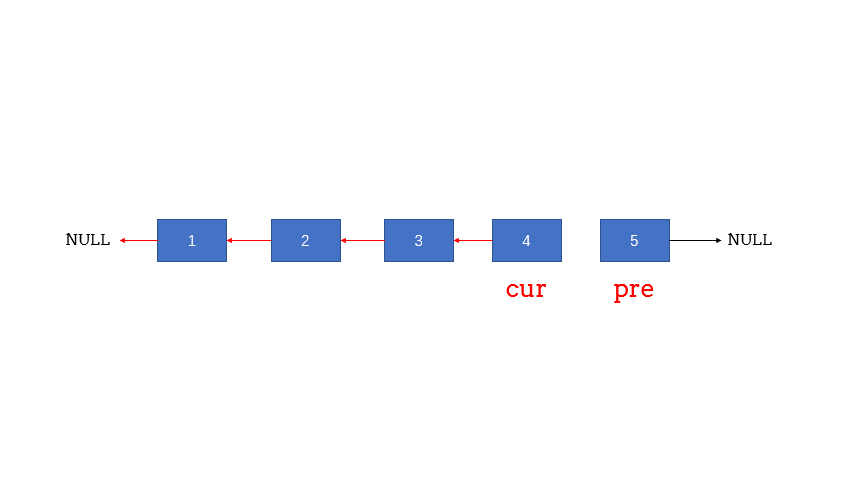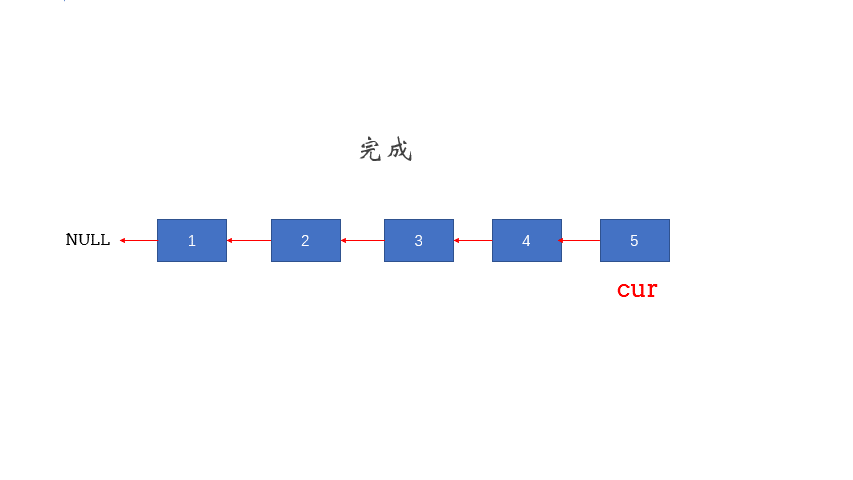
输入: 1->2->3->4->5->NULL
输出: 5->4->3->2->1->NULL
进阶:
你可以迭代或递归地反转链表。你能否用两种方法解决这道题？

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/reverse-linked-list
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

迭代式

图片来源：https://leetcode-cn.com/problems/reverse-linked-list/solution/fan-zhuan-lian-biao-shuang-zhi-zhen-di-gui-yao-mo-/

折叠/查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    /*
    迭代式的翻转链表
    将从第二个节点开始，逐个插入到头节点和第一个节点之间
    */
    ListNode* reverseList(ListNode* head) {
        if(head == nullptr || head->next == nullptr) return head;

        ListNode *prehead = new ListNode(0,head);
        ListNode *next;
        ListNode* cur = head->next;
        head->next = nullptr;//记得将末端置空
        while(cur != nullptr){
            next = cur->next;
            cur->next = prehead->next;
            prehead->next = cur;
            cur = next;
        }
        return prehead->next;
    }
};

递归式

  • 递归的找到最后一个节点，返回，中间不对那个节点做任何处理，单纯的返回，这样就成了第一个节点。
  • head表示每个递归中的当前的那个节点，使得其后一个节点指向它，然后它在指向Null.

图片来源：https://leetcode-cn.com/problems/reverse-linked-list/solution/fan-zhuan-lian-biao-shuang-zhi-zhen-di-gui-yao-mo-/

折叠/查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
ListNode* reverseList(ListNode* head) {

    //递归结束条件, 到最后一个节点
    //head == nullptr只是为了防止整个链表都为空设置的
    if(head == nullptr || head->next == nullptr) return head;
    
    ListNode* ret = reverseList(head->next);//寻找到最终端的节点，作为起始节点
    head->next->next = head;//后一个节点指向前一个节点
    head->next = nullptr;
    return ret; //中间不对ret做任何更改，每次都返回，这样最终尾节点，就成为了头节点
    
}

双指针

思想就是：fast指针指向low指针，局部反转，直到fast走到了末尾。

图片来源：https://leetcode-cn.com/problems/reverse-linked-list/solution/fan-zhuan-lian-biao-shuang-zhi-zhen-di-gui-yao-mo-/

折叠/查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//前后指针
ListNode* reverseList(ListNode* head) {

    if(head == nullptr || head->next == nullptr) return head;

    ListNode * fast= head->next;
    ListNode *low = head;
    low->next = nullptr;

    while(fast != nullptr){
        ListNode * ne = fast->next;
        fast->next = low;
        low = fast;
        fast = ne;
    }

    return low;
}

617 合并二叉树

2021/04/21

给定两个二叉树，想象当你将它们中的一个覆盖到另一个上时，两个二叉树的一些节点便会重叠。

你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠，那么将他们的值相加作为节点合并后的新值，否则不为 NULL 的节点将直接作为新二叉树的节点。

示例 1:

输入:
Tree 1 Tree 2
1 2
/ \ / \
3 2 1 3
/ \ \
5 4 7
输出:
合并后的树:
3
/
4 5
/ \ \
5 4 7
注意: 合并必须从两个树的根节点开始。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/merge-two-binary-trees
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

递归

折叠/查看代码 
1
2
3
4
5
6
7
8
9
10
TreeNode *mergeTrees(TreeNode *root1,TreeNode * root2){
    if(root1 == nullptr || root2 == nullptr){
        return root1 == nullptr ? root2:root1;
    }

    root1->val += root2->val;
    root1->left = mergeTrees(root1->left,root2->left);
    root1->right = mergeTrees(root1->right,root2->right);
    return root1;
}

或者使用广度优先遍历的思想实现，使用两个辅助队列。

剑指 二叉搜索树的最近公共祖先

2021/04/21

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明:

所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉搜索树中。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/er-cha-sou-suo-shu-de-zui-jin-gong-gong-zu-xian-lcof
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

因为是二叉搜索树，所以找到节点的同时，走过的路径就是其对应的祖先节点。

获得全部的祖先节点之后，从后向前找到两个路径中都有的。

  • vector没有提供find方法，使用算法头文件的方法即可。
折叠/查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
    vector<TreeNode *>path1;
    vector<TreeNode*> path2;

    TreeNode *tmp = root;
    while(tmp != p){
        path1.push_back(tmp);
        if(tmp->val > p->val){
            tmp = tmp->left;
        }
        else{
            tmp = tmp->right;
        }
    } 
    path1.push_back(tmp);

    tmp = root;
    while(tmp != q){
        path2.push_back(tmp);
        if(tmp->val > q->val){
            tmp = tmp->left;
        }
        else{
            tmp = tmp->right;
        }
    } 
    path2.push_back(tmp);

    //然后比对两个数据结构
    for(auto it = path1.rbegin();it!= path1.rend();it++){
        auto result = find(path2.begin(),path2.end(),*it);
        if(result != path2.end()){
            return *it;
        }
    }
    return nullptr;
}
  • 另一种思路，巧妙运用二叉搜索树的特性，若当前节点均大于两个节点，当前节点向左，若均小于两个节点，向右。
  • 其他情况下，一大一小，就是中间节点。
  • 这样一次遍历，而且不用去对比和查找。
算法
LeetCode

本博客所有文章除特别声明外，均采用 CC BY-SA 4.0 协议 ，转载请注明出处！