算法题（二）

本文最后更新于：2021年4月8日 晚上

概览：LeetCode刷题。

1
2
3
4
<details>
    <summary>折叠/查看代码</summary>
    
</details>

6 Z字型变换

2021/04/01

将一个给定字符串 s 根据给定的行数 numRows ，以从上往下、从左到右进行 Z 字形排列。

比如输入字符串为 “PAYPALISHIRING” 行数为 3 时，排列如下：

P A H N
A P L S I I G
Y I R
之后，你的输出需要从左往右逐行读取，产生出一个新的字符串，比如：”PAHNAPLSIIGYIR”。

请你实现这个将字符串进行指定行数变换的函数：

string convert(string s, int numRows);

示例 1：

输入：s = “PAYPALISHIRING”, numRows = 3
输出：”PAHNAPLSIIGYIR”
示例 2：
输入：s = “PAYPALISHIRING”, numRows = 4
输出：”PINALSIGYAHRPI”
解释：
P I N
A L S I G
Y A H R
P I

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/zigzag-conversion
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题解

思路比较普通，一个flag来标识是顺序访问还是逆序访问，一个index来表示应当添加到哪个行。

折叠/查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution {
public:
    string convert(string s, int numRows) {

        if (numRows == 1) {
            return s;
        }

        vector<string> vecstr(numRows,"");

        int len = s.size();
        int index = 0;	//对应字符串索引
        bool asc = true;//顺序扫描还是逆序扫描
        for (int i = 0; i < len; i++) {
            vecstr[index].push_back(s[i]);
            if (asc) {
                if (index >= numRows-1) {
                    asc = false;
                    index = numRows-2;
                }
                else {
                    index++;
                }
            }
            else{
                if (index <= 0) {
                    asc = true;
                    index = 1;
                }
                else {
                    index--;
                }
            }

        }

        string result = "";
        for (auto i : vecstr) {
            result += i;
        }

        return result;
    }
};

找出字典序最小的字母组合，保持相对位置 | 【游奕互动笔试】

2021/04/01

给定一个字符串s，返回其 最小字典序 的子字符串，且该子串包含了s中 所有出现的字母，并只出现一次 。如:s=“dbadcdbd”，返回“acbd”。s=“dbbbbbbaaaabbbc”,返回“dabc”

函数声明如下：string GetSubString(string& s);

题解

这道题出自 游奕互动 的笔试题目。

大致思路是要包含全部出现过的字母，然后保持其在序列中的相对顺序，选择字典序排列最小的字符。

字典序：“abc” 的字典序 要小于 “abd”，c在字母表中要先于d.

中间过程：对于bcabc，从头开始扫描，b加入容器，c加入容器，然后读到了a，此时发现c的字典序大于a，并且它在后面还会出现，那么把c抛弃，除此之外，b又比a大，且后面还有，则抛弃b。之后再读入b，c。

这里的过程，符合后进先出，采用栈来存储。

需要确定后面时候还会出现，采用一个map映射，保存其字母对应的次数，抛弃或者加入结果时对应数目自减。

除此之外，还需要知道当前读到的这个字符，在容器之中是否有，毕竟题目要求只需要一份，则如法炮制，也采用map映射，存在置为false。

核心逻辑：当栈不为空，并且当前字符不在栈中，并且栈顶元素大于当前元素同时栈顶元素后面还有。

折叠/查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
string GetSubString(string &s){

    stack<char> charstack;
    map<char,int> charnum;	//不同字母数量
    map<char,bool> instack;//是否在栈中

    //字母数量记录
    int len = s.size();
    for(int i=0;i<len;i++){
        charnum[s[i]]++;	//map的用法，如果不存在则插入，存在则其value值+1
    }

    for(int i=0;i<len;i++){
        char tmp = s[i];

        if(instack[tmp]){	//若在栈中，直接跳过
            charnum[tmp]--;
            continue;
        }

        while(!charstack.empty() && tmp < charstack.top() && charnum[charstack.top()] > 0){
            instack[charstack.top()] = false;
            charstack.pop();
        }

        charstack.push(tmp);
        instack[tmp] = true;
        charnum[tmp]--;
    }

    string result = "";
    while(!charstack.empty()){
        result = charstack.top() + result;//注意栈的顺序！
        charstack.pop();
    }

    return result;
}

atoi的模拟实现

2021/04/02

请你来实现一个 myAtoi(string s) 函数，使其能将字符串转换成一个 32 位有符号整数（类似 C/C++ 中的 atoi 函数）。

函数 myAtoi(string s) 的算法如下：

读入字符串并丢弃无用的前导空格
检查下一个字符（假设还未到字符末尾）为正还是负号，读取该字符（如果有）。 确定最终结果是负数还是正数。 如果两者都不存在，则假定结果为正。
读入下一个字符，直到到达下一个非数字字符或到达输入的结尾。字符串的其余部分将被忽略。
将前面步骤读入的这些数字转换为整数（即，”123” -> 123， “0032” -> 32）。如果没有读入数字，则整数为 0 。必要时更改符号（从步骤 2 开始）。
如果整数数超过 32 位有符号整数范围 [−231, 231 − 1] ，需要截断这个整数，使其保持在这个范围内。具体来说，小于 −231 的整数应该被固定为 −231 ，大于 231 − 1 的整数应该被固定为 231 − 1 。
返回整数作为最终结果。
注意：

本题中的空白字符只包括空格字符 ‘ ‘ 。
除前导空格或数字后的其余字符串外，请勿忽略 任何其他字符。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/string-to-integer-atoi
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

普通思路

做一个循环遍历，

1
2
3
4
5
6
7
8
9
10
11
1.碰到字母以及小数点 立即结束循环
2.碰到空格 
    检查读到过数字或者符号吗？
    读到过，结束循环
    没读到过，继续
3.碰到符号
    之前没读到过符号时设定读到过符号
    之前读到过符号或者数字，结束循环
4.碰到数字
    设定读到过数字
    记录到结果中

对应的就是漫长的代码，很多个flag以及很多的if语句，最终结果是对应超长的数字：超出去long的存储范围的数字就会报错，在漫长的接近两个小时之后，遂放弃。

折叠/查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
class Solution {
public:

    int char2int(char& c) {
        return c - '0';
    }

    int myAtoi(string s) {
        //清除前导空格 留下 0-9 + -

        int len = s.size();
        if (len < 1) {
            return 0;
        }

        long result = 0;
        int index = 0;
        bool neg = false;//默认为正数
        bool isnum = false;
        bool issig = false;
        while (index < s.size()) {
            char tmp = s[index];

            if ((tmp >= 'A' && tmp <= 'Z') || (tmp >= 'a' && tmp <= 'z') || tmp == '.') break;

            //读到空格忽略、
            if (tmp == ' ') {
                //若有数字 或者 读到了符号
                if (!isnum && !issig) { 
                    index++;
                    continue; 
                }
                //读完符号或者数字之后读到了空格
                else break;//可能读到 '-  1'  '123  '
            }

            if ((tmp == '-' || tmp == '+')) {
                if (issig || isnum) break;//防止读到多个符号
                else issig = true;//可能是数字的开始
            }

            if (tmp >= '0' && tmp <= '9') {
                if (!isnum) {
                    //查看其前面那个字符是不是正负号
                    if (index - 1 >= 0 && s[index - 1] == '-') {
                        neg = true;
                    }
                    else {
                        neg = false;
                    }
                    //修改标记为isnum = true;
                    isnum = true;
                }
                result = result * 10 + char2int(tmp);
            }
            index++;
        }

        //判断数值是否大于INT_MAX
        if (result > INT_MAX) {
            return neg ? INT_MIN : INT_MAX;
        }
        return neg ? -result : result;

    }
};
  • 其实不需要对字母或者小数点做额外的判断，只要不符合数字、正负号、空格之外的情况就不会进入对应的判断语句，直接return就好了。
  • 对于数字越界这件事，不应该用long去存储，如果是32位机，long也是32位。。。，对于数字越界应当有额外的判断手段。

修正思路

一个正常的可以解析出数字的字符串大致模样：[一些空格][+|-|无][0-9]~

所以首先用while循环清除空格，之后读取符号，若读到负号则数字为负数，否则为正数。然后就应当读取数字，result = result * 10 + des。

一个比较重要的点是越界的处理，int是有符号数，result*10超出INT_MAX之后，或者刚好等于INT_MAX/10，但是后续的数字加上可能超过INT_MAX，借此来判断其是否越界。

  • 2^ 31 - 1 = 2147483647，INT_MAX / 10 = 214748364，一旦乘以10再加上一个大于7的数字就会越界。
折叠/查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution{

public:

    int myAtoi(string s){

        bool neg = false;
        int result = 0;
        int index = 0;
        int len = s.size();

        while(index < len && s[index] == ' '){
            index++;
        }

        if(index < len && (s[index] == '-' || s[index] == '+')){
            if(s[index] == '-') neg = true;
            index++;
        }

        while(index <len &&(s[index] >= '0' && s[index] <= '9')){
            if(result > INT_MAX / 10 || (result == INT_MAX / 10 && (s[index] - '0') > 7))//溢出
                return neg?INT_MIN:INT_MAX;

            result = result* 10  + (s[index] - '0');
            index++;
        }
        return result *(neg ? -1 : 1);
    }
};

1143 最长公共子序列【动态规划】

21/04/03

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符
（也可以不删除任何字符）后组成的新字符串。

例如，”ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
示例 1：

输入：text1 = “abcde”, text2 = “ace”
输出：3
解释：最长公共子序列是 “ace” ，它的长度为 3 。
示例 2：

输入：text1 = “abc”, text2 = “abc”
输出：3
解释：最长公共子序列是 “abc” ，它的长度为 3 。
示例 3：

输入：text1 = “abc”, text2 = “def”
输出：0
解释：两个字符串没有公共子序列，返回 0 。

提示：

1 <= text1.length, text2.length <= 1000
text1 和 text2 仅由小写英文字符组成。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/longest-common-subsequence
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

刚开始确实没有任何思路，但是发现了一个神奇的网站，有表格来帮助查看动态结果。

https://alchemist-al.com/algorithms/longest-common-subsequence

分析思路：两个字符串对比最长公共子序列，势必要进行的是双层循环，str1的串逐步和st2的每一个逐渐增长的串做对比，记录他们的公共长度。

例如子串：TAGA和子串：AGATGACA。

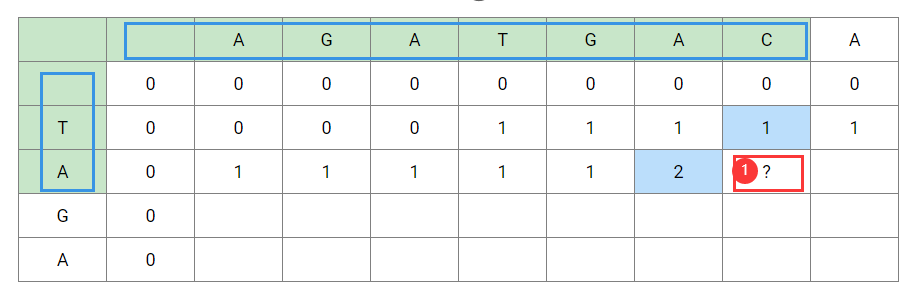
如下图表所示，为了初始化方便，加入一行一列与空值对比的结果，公共子串长度为0.

如图：TA与AGA的最长公共子序列，因为两者的末尾相同，则取决于T与AG的公共子序列的长度再+1即可。

如图：TA与AGATGA的最长公共子序列，因为两者的末尾相同，则取决于T与AGATG的公共子序列的长度再+1即可。

如下图，而当两者当前的这个字符不相等时，其最长公共子序列取决于TA与AGATGA的公共长度和T与AGATGAC的公共长度的最大值。

当整个表格遍历完成时，就得到了两个字符串的最长公共子序列的长度。

这也就是动态规划的思想。现有的判断，基于原来的判断再加上一点新的判断

1
2
3
4
5
if(str1[row-1] == str2[col-1]){
	dp[row][col] = dp[row-1][col-1] + 1;
}else{
	dp[row][col] = max(dp[row][col-1],dp[row-1][col]);
}

解法

折叠/查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int len1 = text1.size(), len2 = text2.size();

        vector<vector<int> > dp(len2+1,vector<int>(len1+1));
        //text1 横向，text2纵向
        for (int j = 1; j <= len2; j++) {
            for (int i = 1; i <= len1; i++) {
                if (text1[i - 1] == text2[j - 1]) {
                    dp[j][i] = dp[j - 1][i - 1] + 1;
                }
                else {
                    dp[j][i] = max(dp[j - 1][i], dp[j][i - 1]);
                }
            }
        }
        return dp[len2][len1];
    }
};

动态规划，妙不可言。

11 乘最多水的容器【双指针】

21/04/04

给你 n 个非负整数 a1，a2，…，an，每个数代表坐标中的一个点 (i, ai) 。
在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0) 。
找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器。

输入：[1,8,6,2,5,4,8,3,7]
输出：49
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。
示例 2：

输入：height = [1,1]
输出：1
示例 3：

输入：height = [4,3,2,1,4]
输出：16
示例 4：

输入：height = [1,2,1]
输出：2

n = height.length
2 <= n <= 3 * 104
0 <= height[i] <= 3 * 104

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/container-with-most-water
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

暴力解法

找出所有柱子的可能组合，然后求得其最大值。当然时间超限。O(n^2)的复杂度。

双指针法——削减解空间

对于最左右两根柱子，假设左边的比较短，如果右边的柱子随意更换，其宽度都小于原来，同时由于左边的柱子短，所以其新构成的体积均会小于原来的体积。
–> 由此得出，包含左边柱子的全部情况中，最初始的情况是体积最大的。

所以思想就是，每次消去两根柱子中最短的那根对应的全部解空间，中间使用max来记录，最大值当搜索的两根柱子的指针碰到一起的时候，停止搜索。

https://leetcode-cn.com/problems/container-with-most-water/solution/on-shuang-zhi-zhen-jie-fa-li-jie-zheng-que-xing-tu/

折叠/查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
public:
    int maxArea(vector<int>& height) {
        int maxarea = 0;
        int i = 0;
        int j = height.size() - 1;

        while (i < j) {
            int area = (j - i)*min(height[i], height[j]);
            maxarea = max(maxarea, area);
            if (height[i] < height[j]) {
                i++;
            }
            else {
                j--;
            }
        }
        return maxarea;
    }
};

42 接雨水【单调栈】

2021/04/05

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/trapping-rain-water
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路：单调递减栈。

接雨水就是一个很经典的单调递减栈的问题。

单调递减栈：

  • 单调递减栈就是栈内元素保持单调递减的栈。
  • 操作规则：如果新元素比栈顶元素小，就入栈，如果新元素比较大，那就把栈内元素弹出来，直到栈顶元素比新元素大。
  • 对于单调递减栈，当元素出栈的时候，说明这个新元素是出栈元素向后找的第一个比其大的元素。同理也说明 新的栈顶元素是出栈元素向前找第一个比其小的元素。

模板：

可以使用栈存储数组索引或者直接存储值。

1
2
3
4
5
6
7
8
stack<int> st;

for(int i=0;i<nums.size();i++){
	while(!st.empty() && num[st.top()] < num[i]){//while循环将一直工作
		st.pop();
	}
	st.push(i);
}

解法

https://leetcode-cn.com/problems/trapping-rain-water/solution/trapping-rain-water-by-ikaruga/

当读到大于栈顶的元素时，这是就需要弹栈，保持栈的规则。所以计算雨水的量的问题就在弹栈之后的代码中。

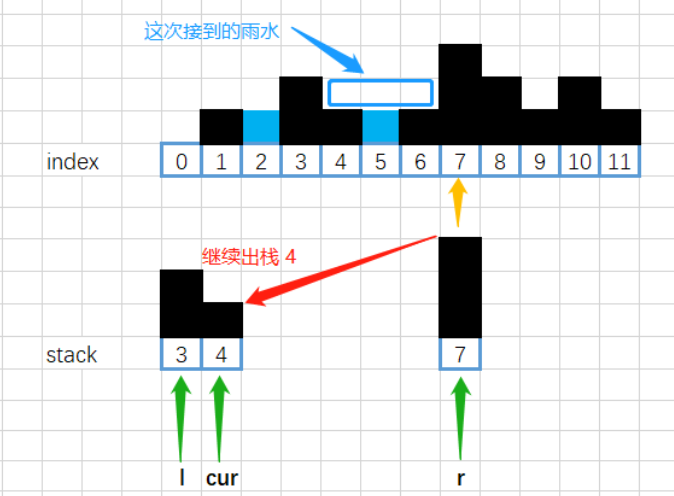
计算方法：获取当前新元素的索引，以及栈顶的前一个元素的索引，由此来计算出宽度，而至于高度，就像是上一个乘水容器计算一样，获取左右两个柱子的高度，减去当前栈顶元素的高度，就是水的高度。

巧妙地计算方法：先cur记录当前元素索引，然后出栈，则栈顶元素就变成了左边柱子，当前读到地元素就是右边柱子。因为栈中记录的是索引，对于上面倒数第二幅图，看似形状不正确，但是逻辑正确。

雨水计算逻辑

1
2
3
4
5
6
7
8
9
10
11
12
13
int result = 0;//雨水

while(!st.empty() && height[st.top()] < height[i]){
    int cur = st.top();//记录出栈的块，一边访问其高度
    st.pop();
    if(st.empty()) break;//注意！！！
    
    
    int left = st.top();//左边柱子
    int right = i;//当前柱子就是右边柱子
    int hei = min(height[right],height[left]) - height[cur];
    result += (right - left -1) * hei;
}

整体代码：

折叠/查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    int trap(vector<int>& height) {
        int len = height.size();
        if (len < 3) {	//特殊情况，直接排除
            return 0;
        }
        stack<int> st;//存储数组索引
        int result = 0;//最终结果

        for (int i = 0; i < len; i++) {
            while (!st.empty() && height[st.top()] < height[i]) {
                int cur = st.top();
                st.pop();
                if (st.empty()) break;
                int left = st.top();
                int right = i;
                int he = min(height[right], height[left]) - height[cur];//左右两边最小高度 - 当前节点的高度
                result += (right - left - 1) *he;
            }
            st.push(i);//若满足递减栈则直接插入
        }
        return result;
    }
};

14 最长公共前缀

2021/04/05

编写一个函数来查找字符串数组中的最长公共前缀。

如果不存在公共前缀，返回空字符串 “”。

示例 1：
输入：strs = [“flower”,”flow”,”flight”]
输出：”fl”
示例 2：

输入：strs = [“dog”,”racecar”,”car”]
输出：””
解释：输入不存在公共前缀。

提示：

0 <= strs.length <= 200
0 <= strs[i].length <= 200
strs[i] 仅由小写英文字母组成

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/longest-common-prefix
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

思路：循环比较，若某个字符不等，则返回结果，可以选择第一个子串作为比较的串，其他串都与这个串做比较，合适的话加入结果集合，不合适直接退出。

折叠/查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    string longestCommonPrefix(vector<string>& strs) {
        int len = strs.size();
        if (len == 0) return "";
        if (len == 1) return strs[0];

        string result = "";
        string ans = strs[0];//选择作为对比串
        int anslen = ans.size();
        for (int i = 0; i < anslen; i++) {
            for (int j = 1; j < len; j++) {
                if (ans[i] != strs[j][i]) {
                    return result;      //不能使用break，它只能跳出一个循环
                }
            }
            result.push_back(ans[i]);
        }
        return result;
    }
};

获得有向边输出单链表 | 【偶数科技笔试】

2021/04/06

输入一系列有向边，判断其是否构成一个单向链表。若构成单向链表，则输出该单向链表的反向形式。若不构成，输出NO。

Input
每行为一条有向边src dst，以空格分隔出发点和到达点。src和dst可能为字符串，输入以EOF结束。
Output
情况1：每行一个点名，输出该单向链表的反向形式。
情况2：NO

Sample 1

Input
个 一
是 这
句 个
。 子
一 是
子 句

Output

这
是
一
个
句
子
。

要通过值去查找元素，所以最好使用哈希表，unordered_map。

在获取输入的时候，若某个节点重复，可知这个链表失败，或者最后形成了环，这就是所有节点中无出现一次的节点，这时也可以直接排除。

巧妙地找到左边的头节点，由此递推向后去查找，将找到的值压入栈，同时删除哈希表元素。

若某个元素找不到，说明不连续，若直到哈希表空的时候都没出问题，那就成功了。

折叠/查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
#include <iostream>
#include <vector>
#include <map>
#include <string>
#include <unordered_map>
#include <algorithm>
#include <stack>
using namespace std;
string gethead(unordered_map<string, string> &nums, map<string, int> &nums2) {
    //获取头部节点
    //找出次数为一的节点
    map<string, int>::iterator it = nums2.begin();
    for (; it != nums2.end(); it++) {
        if (it->second == 1 && nums.find(it->first) != nums.end()) {
            return it->first;
        }
    }
    return "";
}
string work(string &head, unordered_map<string, string> &nums) {
    //从头部节点开始
    stack<string> st;
    st.push(head);
    string next = nums[head];
    st.push(next);
    nums.erase(head);
    while (!nums.empty()) {
        //寻找下一个节点，然后入栈
        string tmp = next;
        if (nums.find(next) == nums.end()) {
            return "NO";
        }
        next = nums[next];
        st.push(next);
        nums.erase(tmp);
    }
    //输出结果
    string result = "";
    while (!st.empty()) {
        result = result + st.top()+"\n";
        st.pop();
    }
    return result;
}
int main() {
    unordered_map<string, string> nums;
    unordered_map<string, string> nums1;
    map<string, int> nums2;
    int i = 0;
    string str1, str2;
    str1.clear();
    str2.clear();
    bool flag = true;

    //左右数据均不能重复，重复说明有环
    while (cin >> str1 >> str2)//空格可以区分数据
    {
        if (str1== str2) {
            flag = false;
        }

        if (nums.insert(make_pair(str1, str2)).second == false) {
            flag = false;
        }
        if (nums1.insert(make_pair(str2, str1)).second == false) {
            flag = false;
        }

        nums2[str1]++;
        nums2[str2]++;

        //插入成功就继续
        str1.clear();
        str2.clear();
        i++;
        if (i == 6) {
            break;
        }
    }

    //处理数据
    //循环map去重
    if (flag == false) {
        cout << "NO" << endl;
        return 0;
    }

    string head = gethead(nums,nums2);
    if (head == "") {//没有重复的点
        cout << "NO" << endl;
        return 0;
    }
    cout << work(head, nums) << endl;
    return 0;
}

77 组合 【回溯】

2021/04/07

给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。

示例:

输入: n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/combinations
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

经典的回溯解法，一般最好画一个树，查看其访问路径。

回溯一般就是与递归相互挂钩的，其本身就是一种暴力穷举的过程。

回溯框架

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void trackback(参数){
	if(终止条件){	//树搜索到了叶子时 就存储结果，返回
		存放结果
		return;
	}
	
	//for循环 横向遍历
	for(选择：本层集合中元素){
		处理节点，比如记录路径;
		trackback(路径，选择列表);//递归 纵向遍历
		回溯，撤销上一步记录的结果;
	}

}
  • 终止条件：记录的元素个数达到了要求的数量
  • 剪枝：若当前需要的元素个数大于了还能选择的个数，就没必要再递归了。
  • 参数：由于我们要的是当前节点选择之后，其后面节点的组合，所以需要一个开始位置，表明我们应当从哪里找。
  • 处理节点：使用一个数组记录路径，达到了条件就存储进入最终结果集。
折叠/查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    void trackback(int n,int k,int start,vector<vector<int>> &result,vector<int> &path){
        //结束条件 还需要的数 小于 还有的数
        if( k - path.size() > n-start+1)
            return;
        if(path.size() == k){
            result.push_back(path);
            return;
        }
        //横向遍历
        for(int i=start;i<=n;i++){
            path.push_back(i);
            trackback(n,k,i+1,result,path);//递归，纵向遍历
            path.pop_back();
        }
    }

    vector<vector<int>> combine(int n, int k) {
            vector<vector<int>> result;
            vector<int> path;
            trackback(n,k,1,result,path);
            return result;
    }
};

此外另一种更好的优化思路：剪枝操作直接在for循环中来进行处理：

  • 至多能刚好凑够一次结果时应当所处的位置：n - (k-path.size()) + 1
    • 例如当前元素0个，需要两个元素，则至少要从3号位置开始。
1
2
3
4
//还需要1个元素 遍历到n-1就可以
for(int i=start; i<= n-(k-path.size()) +1;i++){
...
}

46 全排列【回溯】

2021/04/07

给定一个 没有重复 数字的序列，返回其所有可能的全排列。

示例:

输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/permutations
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

依旧是很经典的回溯问题，但是不同于上一个组合问题，这里的细节又发生了变化。

全排列时，要看当前数据有没有被使用过，它要搜索全部的数据，然后找出一个没有被使用过的数据，所以每次横向搜索都是完全遍历，使用辅助数组来标记是否被使用，若被使用，就立即结束当前的循环。

折叠/查看代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    void trackback(vector<int> &nums,vector<vector<int>> &result,vector<int> &path,vector<int> &used){
        if(path.size() == nums.size()){
            result.push_back(path);
            return;
        }
        for(int i=0;i<nums.size();i++){
            if(used[i] == 1) continue;//若使用过了，就跳过
            used[i] = 1;
            path.push_back(nums[i]);

            trackback(nums,result,path,used);

            path.pop_back();
            used[i] =0;

        }

    }
    vector<vector<int>> permute(vector<int>& nums) {

        vector<vector<int>> result;
        vector<int> used(nums.size(),0);//记得初始化
        vector<int> path;

        trackback(nums,result,path,used);
        return result;
    }
};