插入排序算法——直接插入、折半插入、希尔排序

本文最后更新于：2021年1月8日 上午

概览：插入排序算法思想以及C++代码的实现。

插入排序

算法思想：每次将⼀个待排序的记录按其关键字大小插入到前面已排好序的子序列中，直到全部记录插⼊完成。

即通过逐步构造局部有序，来最终到达全局有序。

起始时刻，可将第一个元素当作最初的有序子序列，然后逐步增加元素构成信息的有序子序列。

直接插入排序

即插入排序最直接的实现方式。默认按照从小到大的顺序排序，从前向后逐步构造有序序列。

只有当前待排序元素小于其前面的元素时才需要排序，否则直接插入即可。

分为无哨兵版和带哨兵版。

哨兵：对于数组这样顺序存储的从0开始存储的数据结构，可将第0个位置来存储哨兵，来减少代码中判定的复杂度。看代码比较直接。

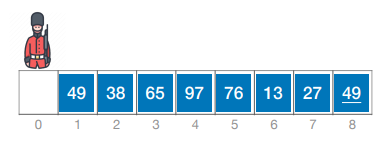
无哨兵版

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void InsertSort(int A[],int n){
	int temp;//临时变量，暂存数据
	int i, j;

	for (i = 1; i < n; i++) {		//对A[1]到A[n-1]上的元素进行插入排序
		if (A[i] < A[i-1]) {		//若待排序元素小于其前面有序序列的最后一个元素
			temp = A[i];
			for (j = i-1; j >= 0 && A[j] > temp; j--) {
				A[j+1] = A[j];		//所有大于temp的均向后移动
			}
			A[j+1] = temp;			//对应的插入位置
		}
	}
}
  • i从1开始，将0号元素当作初始的有序序列。

带哨兵版

1
2
3
4
5
6
7
8
9
10
11
12
void InsertSort(int A[], int n) {
	int i, j;
	for (i = 2; i <= n; i++) {		//对A[2]到A[n]上的元素进行插入排序
		if (A[i] < A[i-1]) {		//若待排序元素其前面有序序列的最后一个元素
			A[0] = A[i];			//哨兵暂存
			for (j = i-1; A[0] < A[j]; j--) {
				A[j+1] = A[j];	//向后挪位
			}
			A[j+1] = A[0];		//复制到插入位置
		}
	}
}
  • 哨兵就是将数组的0号位置作为暂存元素区，同时在for循环中作为最终的条件判断语句，当A[0]<A[j]时继续向前查找元素，最终停止的条件是j=0时此时表示查到了尽头；而在无哨兵版则既需要判定j的范围又要比较数据大小。

算法分析

  • 空间复杂度：O(1)，著需要常量个辅助空间。
  • 时间复杂度：
    • 最好情况下，初始就有序，那就是n个元素进行n-1趟处理，每次只需比关键字n-1次，O(n)。
    • 最坏情况下，初始为逆序，
      • 第一趟：对比关键字2次(for循环内部)，移动3次(哨兵暂存，元素移位，插入位置)，
      • 第二趟：对比关键字3次，移动4次
      • …
      • 第n-1趟：对比关键字n次，移动n+1次
      • 一共对比$$\frac{(n+2)(n-1)}{2}$$ ,一共移动$$\frac{(n+4)(n-1)}{2}$$（等差数列计算）
      • O(n^2).
    • 平均情况下，即随机排列
      • 比较次数$$\frac{(n+2)(n-1)}{4}$$，移动次数$$\frac{(n+4)(n-1)}{4}$$
      • O(n^2).
  • 直接插入算法是稳定的算法。即当待排序序列中有多个相同的元素时，排序之后这几个元素的相对次序仍不变。
  • 算法评价：简单、容易实现，适用于待排序序列比较小或者基本有序的情况。
  • 算法适用：可用于顺序表、链表这样的数据结构。

折半插入排序

算法思想：折半插入排序是对直接插入排序的一种优化，即采用折半查找这种方式找到应该插入的位置，再移动元素。

与直接插入排序相比，折半查找这种方式可以减少比较的次数，但是移动元素的次数没有发生变化。

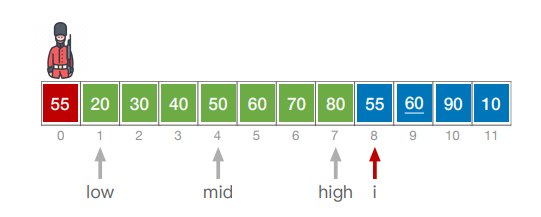
使用折半查找的规则来进行查找，不过不是为了找到该元素，而是要找到比该元素都大的元素。

这里使用了A[0]作为哨兵，当low>high的时候停止查找，此时将[low,i-1]内的元素全部右移，然后将A[0]移动到low所指的位置。

而当A[mid] == A[0]时，为了保证算法的稳定性，应当在mid的右边继续寻找插入位置。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void BinaryInsertSort(int A[],int n) {
	int temp;
	for (int i = 1; i < n; i++) {
		temp = A[i];		//暂存
		int low = 0;
		int high = i-1;		//折半查找范围
		while (low <= high) {
			int mid = (low + high) / 2;
			if (A[mid] > temp) high = mid - 1;//查左半表
			else low = mid + 1;				//查右半表
		}
		for (int j = i - 1; j >= low; j--)
			A[j + 1] = A[j];
		A[low] = temp;	//插入
	}
}

这是非哨兵版本，哨兵实现差别不大。

算法分析

  • 由于只是通过折半查找减少了比较次数，但数据的移动并没有减少，故时间复杂度仍旧是O(n^2)。
  • 算法适用：由于折半查找的限制，这种算法只能用于有序的顺序表，即拥有随机访问特性的数据结构。

希尔排序

算法思想：先追求表中元素部分有序，再逐渐逼近全局有序。

即通过增量d来将待排序的表分割为若干个待排序的特殊子表，例如：A[i],A[i+d],A[i+2d],…,A[i+nd]构成了一个子表，然后对这些子表进行直接插入排序。

然后逐步缩短增量d，重复上述的过程，直到d=1为止。d=1时进行的就是整个表的直接插入排序，并且由于整个表基本有序，非常适用于直接插入排序。

  • 对于增量d的通常做法是每次将增量缩小一半。
1
2
3
4
5
6
7
8
9
10
11
12
13
void ShellSort(int A[], int n) {
	int i, j, temp;
	for (int d = n/2; d >= 1; d = d/2) {//步长
		for (i = d; i < n; i++) {	//从每个子序列的第二个元素开始
			temp = A[i];	//暂存
			if (A[i-d] > temp) {
				for (j = i-d; j >= 0 && A[j] > temp; j-=d)
					A[j+d] = A[j];	//元素后移
				A[j+d] = temp;//插入元素
			}
		}
	}
}

算法分析

  • 空间复杂度：O(1)
  • 时间复杂度：和增量序列d1, d2, d3… 的选择有关，⽬前⽆法⽤数学⼿段证明确切的时间复杂度最坏时间复杂度为 O(n^2)，当n在某个范围内时，可达O(n^1.3).
  • 希尔排序算法不稳定。
    • eg: 65 50 50 ，初始d=2时，两个50的先后次序就会发生错位。
  • 算法适用：顺序表这种可以随机访问的数据结构。

函数调用示例

1
2
3
4
5
6
7
int main(){
	int A[8] = { 49,38,65,97,76,13,27,45 };
	ShellSort(A, 8);
	for (int i = 0; i < 8;i++) {
		cout << A[i] << " ";
	}
}