本文最后更新于:2019年11月14日 晚上

着实头大
学习视频来源 网易云课堂:2018NEUQ-ACM蓝桥杯培训
DFS——Depth Fiest Search
对每一个可能的路径深入到不能深入为止,且每一个节点只能访问一次。
案列:1-n的全排列
如1-3的全排列为 123、132、213、231、312、321
类似于n个标号为1-n的小球放入标号1-n的盒子中,共有多少种方法?
如何往盒子中放球?
1
2
3
4
| for(int i=1;i<=n;i++)
{
a[step]=i;
}
|
a数组表示盒子,step表示第几个盒子,上述表示将第i个球放入第step个盒子中。
如何判断哪些球被放过了?
1
2
3
4
5
6
7
8
| for(int i=1;i<=n;i++)
{
if(book[i]==0)
{
a[step]=i;
book[i]=1;
}
}
|
增加标记数组来标记哪些小球被放过了。
如何继续处理下一个盒子?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| void dfs(int step)
{
for(int i=1;i<=n;i++)
{
if(book[i]==0)
{
a[step]=i;
book[i]=1;
dfs(step+1);
book[i]=0;
}
}
return;
}
|
封装为函数,使用递归进行处理。
如何判断一次排列的结束?
1
2
3
4
5
6
| if(step==n+1)
{
for(int i=1;i<=n;i++)
cout<<a[i];
cout<<endl;
}
|
如果站在第i+1个盒子面前时,说明前n个盒子已经放好球了。则结束
完整代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| #include <iostream>
using namespace std;
int a[1000],book[1000],n;
void dfs(int step)
{
if(step==n+1)
{
for(int i=1;i<=n;i++)
{
cout<<a[i];
}
cout<<endl;
return;
}
for(int i = 1;i<=n;i++)
{
if(book[i]==0)
{
a[step] = i;
book[i] = 1;
dfs(step+1);
book[i]=0;
}
}
return;
}
int main()
{
cin>>n;
dfs(1);
return 0;
}
|
蓝桥杯真题——方格填数
题目描述:
如下的10个格子

填入0~9的数字。要求:连续的两个数字不能相邻。
(左右、上下、对角都算相邻)
一共有多少种可能的填数方案?
请填写表示方案数目的整数。
注意:你提交的应该是一个整数,不要填写任何多余的内容或说明性文字。
题解
读题目即是0-9的全排列,然后根据特定情况筛选。为了方便使用,把0-9换为1-10的序列。
根据上面的模板,数值赋值部分不变,只需要改变逻辑判断的部分,用来方格填数的逻辑判断。
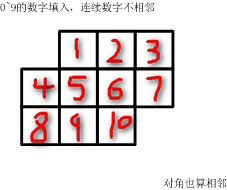
参照底下逻辑判断的代码,非常容易理解。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
| #include <iostream>
#include <math.h>
#include <stdlib.h>
using namespace std;
int cnt = 0;
int a[15],book[15];
void dfs(int step)
{
bool isa = true;
if(step == 11)
{
for(int j=1;j<=2;j++)
{
if(abs(a[j]-a[j+1]) == 1) isa = false;
}
for(int j=4;j<=6;j++)
{
if(abs(a[j]-a[j+1]) == 1) isa = false;
}
for(int j=8;j<=9;j++)
{
if(abs(a[j]-a[j+1]) == 1) isa = false;
}
for(int j=1;j<=6;j++)
{
if(abs(a[j]-a[j+4]) == 1) isa = false;
}
for(int j=1;j<=3;j++)
{
if(abs(a[j]-a[j+3]) == 1) isa = false;
}
for(int j=5;j<=7;j++)
{
if(abs(a[j]-a[j+3]) == 1) isa = false;
}
for(int j=1;j<=2;j++)
{
if(abs(a[j]-a[j+5]) == 1) isa = false;
}
for(int j=4;j<=5;j++)
{
if(abs(a[j]-a[j+5]) == 1) isa = false;
}
if(isa == true) ++cnt;
return;
}
for(int i=1;i<=10;i++)
{
if(book[i]==0)
{
a[step] = i;
book[i] = 1;
dfs(step+1);
book[i] = 0;
}
}
return;
}
int main()
{
dfs(1);
cout<<cnt<<endl;
return 0;
}
|
答案
1580种
蓝桥杯真题——方格分割
题目描述:
6x6的方格,沿着格子的边线剪开成两部分。
要求这两部分的形状完全相同。
如图:

就是可行的分割法。
试计算:
包括这3种分法在内,一共有多少种不同的分割方法。
注意:旋转对称的属于同一种分割法。
请提交该整数,不要填写任何多余的内容或说明文字。
题解
6x6的方格,剪为两部分,一定会经过中心点,并且中心对称。要计算出所有的可能,就需要DFS。
当然需要注意两点,以中心点为出发点向周围进行dfs,所以中心点的状态是被访问过的。
另外由于是正方形,且中心对称,最后的结果要除以4。
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| #include <iostream>
using namespace std;
int book[10][10];
int cnt = 0;
int dir = {1,0,-1,0,0,1,0,-1};
void dfs(int x,int y)
{
if(x==0||x==6||y==0||y==6)
{
++cnt;
return;
}
for(int i=0;i<4;i++)
{
int nx = x+dir[i][0];
int ny = y+dir[i][1];
if(nx<0||nx>6||ny<0||ny>6) continue;
if(book[nx][ny]==0)
{
book[nx][ny]=1;
book[6-nx][6-ny]=1;
dfs(nx,ny);
book[nx][ny]=0;
book[6-nx][6-ny]=0;
}
}
}
int main()
{
book[3][3] = 1;
dfs(3,3);
cout << cnt/4 << endl;
return 0;
}
|
答案
509



